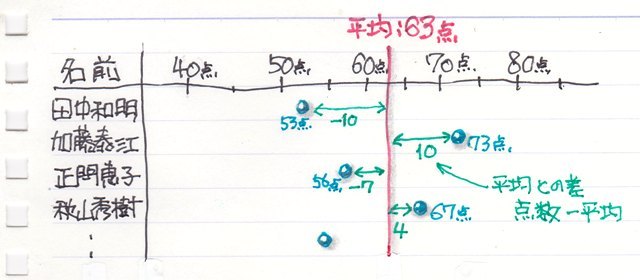
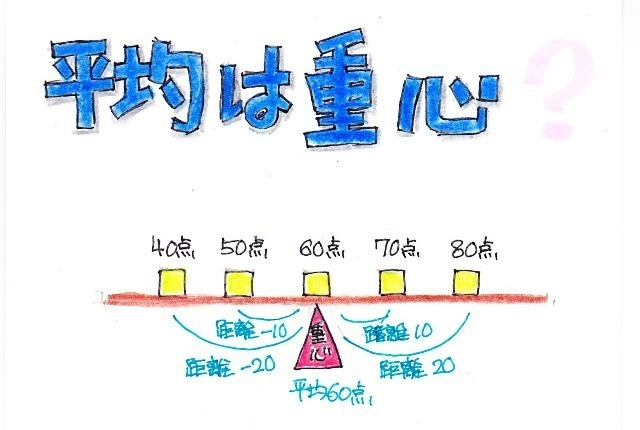
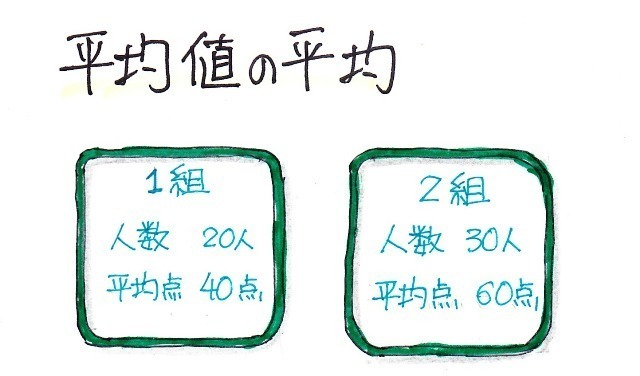
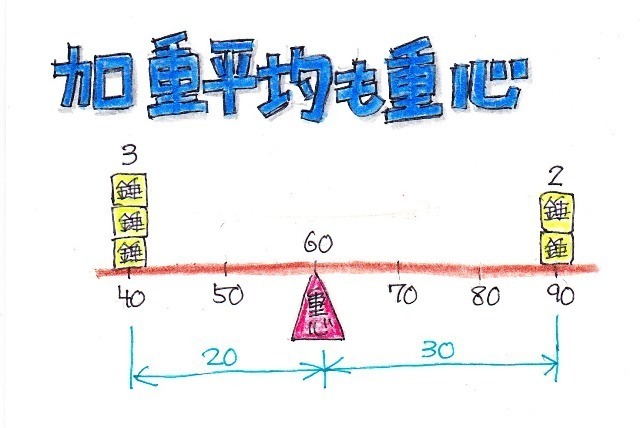
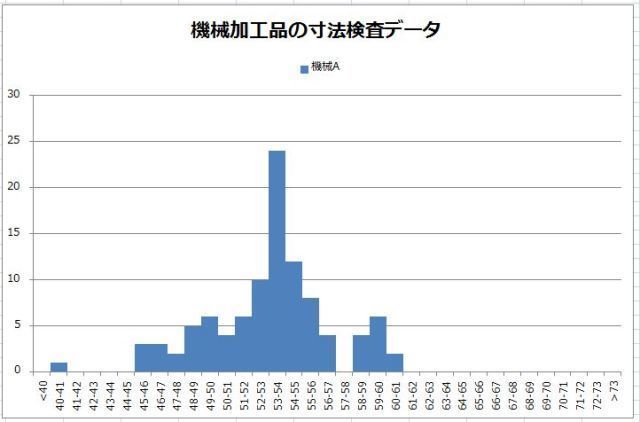
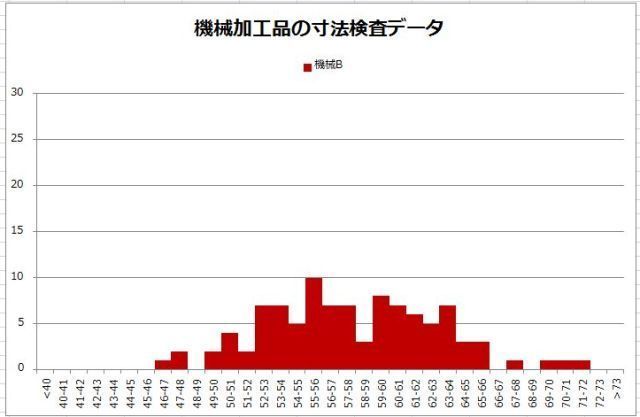
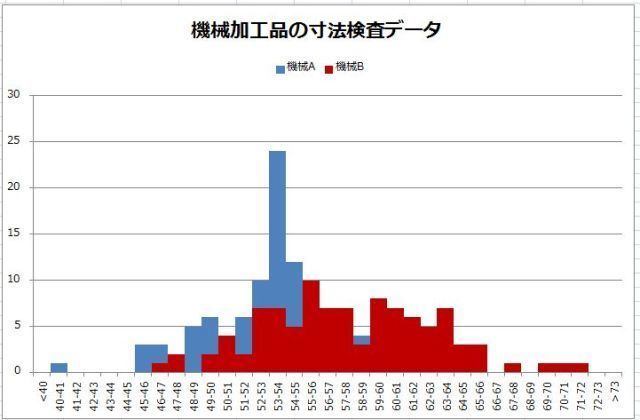
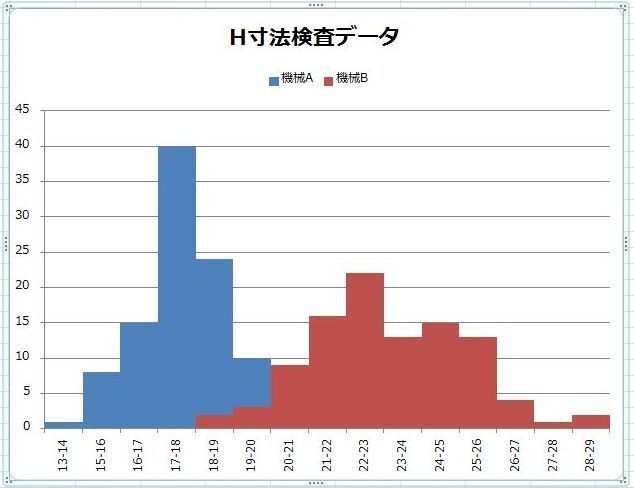
���ϒl���O��l���̉e�����Ă��܂��ꍇ�A
���ϒl���������l�̕�����\�l�Ƃ��ēK���ł��邱�Ƃ�O��������܂������A����ł͂���ɂ��Ă͂ǂ��ł��傤���H
����̑�\�l"
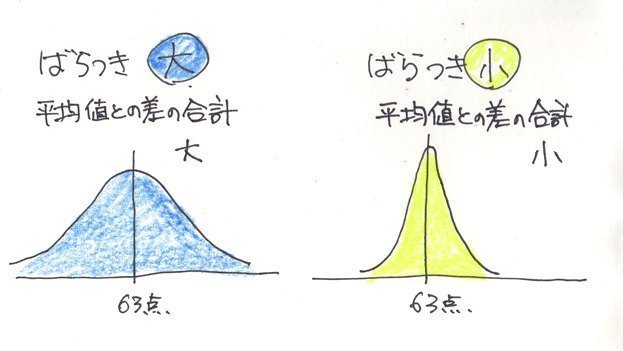
�W����"�����ϒl�Ɠ������W�c�̃f�[�^���z��
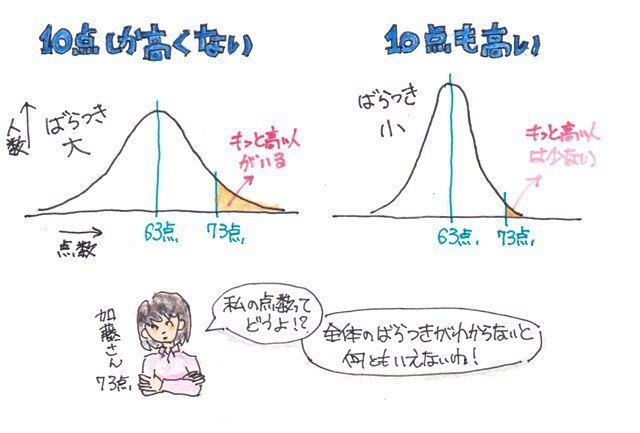
���K���z�ɋ߂��ꍇ�ɗL���Ȓl�ɂȂ�܂��B�ƌ����̂��A�W���������ϒl�ƃf�[�^�̍�������Ƃ��Ă��邽�߂ł��B
�����ŁA�f�[�^�̕��z�����K���z�łȂ��悤�ȏꍇ�ł��ȒP�ɂ���̏�Ԃ�]������̂��A"�l���ʐ��iQuartile�j"�܂���"�l���ʓ_�iQuartile point�j"�A"�l���ʔ͈́iInterquartile range / IQR�j"�A"�l���ʕ��iQuartile deviation�j"�ɂȂ�܂��B
�Ȃ̂ŁA�����l���\�l�Ƃ���ꍇ�́A����͎l���ʕ����\�l�Ƃ��܂��B
�l���ʐ��̓f�[�^���ŏ��l����ő�l�܂ŏ��ɕ��ׂ�4�����i25%���j�������A
��P�l���ʐ��iQ1�j�F25%�̒l
��Q�l���ʐ��iQ2�j�F50%�̒l�i�����l�j
��R�l���ʐ��iQ3�j�F75%�̒l
�Ƃ��܂��B
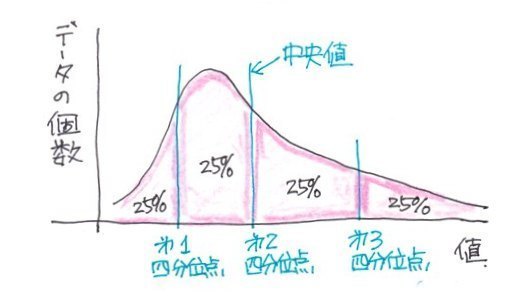 �l���ʐ��i�_�j�̋��ߕ�
�l���ʐ��i�_�j�̋��ߕ��l���ʐ��i�_�j�̋��ߕ��͎��͐F�X����̂ł����A���̃T�C�g��Excel�����s��i�Ƃ����T�C�g�Ȃ̂�Excel��
QUARTILE�����x�[�X�Ƃ������ߕ��Ő������܂��B
�����_�i���̒����̕����j�����߂���@���g�p���Ă��܂��B
����́A���Z�̐��w�T�ŋ������Ă���l���ʐ��Ƃ͈قȂ�܂��B���w�T�̎l���ʐ��͌�قǐ����������܂��B�B
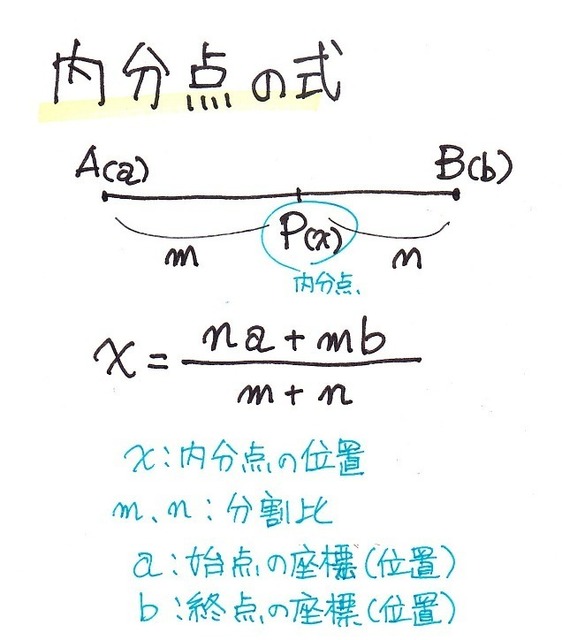
�����_�ƌ����̂͑S�́i�f�[�^�̌��Fn�j��a�Fb�ɕ������鎞�A���̕����_q��
q=�ibx1�{axn)/(a�{b)
�ŋ��߂��܂��B
�܂�l���ʐ��̏ꍇ�͑S�̂�4��������̂ŁA��1�l���ʓ_q1��1:3�ɕ�������_�A��2�l���ʓ_��2:2�ɕ�������_�A��3�l���ʓ_��3:1�ɕ�������_�Ƃ������ƂɂȂ�܂��B
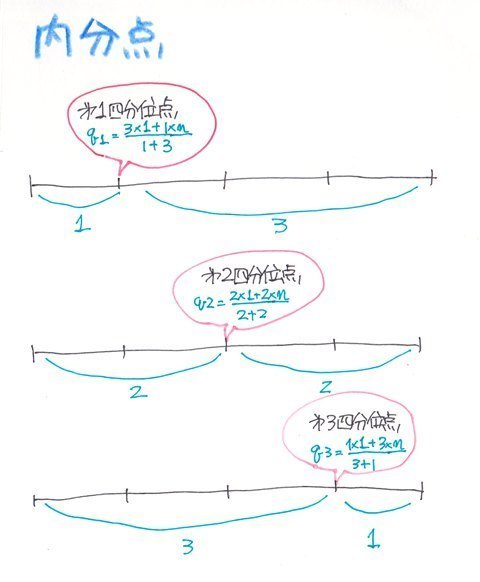 �f�[�^�̌��������̏ꍇ
�f�[�^�̌��������̏ꍇ�f�[�^�̐���8�̏ꍇ�����߂Ă݂܂��B
��1�l���ʐ��i�_�j�̓f�[�^�̌���1:3�ɕ�����������_�ɂȂ�̂�
q1=�i
3x1�{
1x
8)/(
1�{
3)=2.75
�ŏ��l����2.75�Ԗڂ̃f�[�^
��2�l���ʐ��i�_�j�̓f�[�^�̌���2:2�ɕ�����������_�Ȃ̂�
q2=�i
2x1�{
2x
8)/(
2�{
2)=4.5
�ŏ��l����4.5�Ԗڂ̃f�[�^
��3�l���ʐ��i�_�j�̓f�[�^�̌���3:1�ɕ�����������_�Ȃ̂�
q3=�i
1x1�{
3x
8)/(
3�{
1)=6.25
�ŏ��l����6.25�Ԗڂ̃f�[�^
�ƂȂ�܂��B
������₷���}�ɂ��Ă݂�ƁA1����8�̊ԁA�܂�7��4��������_�ƂȂ�̂��킩��܂��B
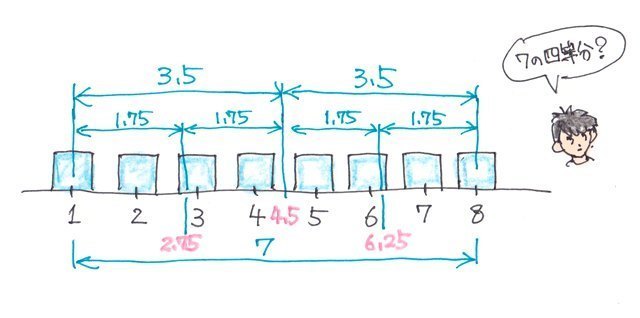
q1=1+1.75=2.75
q2=2.75�{1.75=4.5
q3=4.5+1.75=6.25
�ƂȂ�킯�ł��B�B�B
���āA����8�̃f�[�^��
�P�A�Q�A�V�A�P�O�A�P�P�A�P�T�A�P�W�A�Q�O�Ƃ���ƁA
�܂�Q1��2.75�Ԗڂ̒l�ł����A2�Ԗڂ̃f�[�^��"2"�A3�Ԗڂ̃f�[�^��"7"�Ȃ̂�
Q1=2�{(7-2)��0.75��5.75
Q2��4.5�Ԗڂ̒l�́A4�Ԗڂ̃f�[�^��"10"�A5�Ԗڂ̃f�[�^��"11"�Ȃ̂�
Q2=10+(11-10)��0.5��10.5
Q3��6.25�Ԗڂ̒l�́A6�Ԗڂ̃f�[�^��"15"�A�V�Ԗڂ̃f�[�^��"18"�Ȃ̂�
Q3=15+(18-15)��0.25��15.75
�ƂȂ�܂��B
�f�[�^�̌�����̏ꍇ���x�̓f�[�^�̌������7�̏ꍇ�ł��B
��1�l���ʐ��i�_�j�̓f�[�^�̌���1:3�ɕ�����������_�ɂȂ�̂�
q1=�i
3x1�{
1x
7)/(
1�{
3)=2.5
�ŏ��l����2.5�Ԗڂ̃f�[�^
��2�l���ʐ��i�_�j�̓f�[�^�̌���2:2�ɕ�����������_�Ȃ̂�
q2=�i
2x1�{
2x
7)/(
2�{
2)=4
�ŏ��l����4�Ԗڂ̃f�[�^
��3�l���ʐ��i�_�j�̓f�[�^�̌���3:1�ɕ�����������_�Ȃ̂�
q3=�i
1x1�{
3x
7)/(
3�{
1)=6.25
�ŏ��l����5.5�Ԗڂ̃f�[�^
�ƂȂ�܂��B
������₷���}�ɂ��Ă݂�ƁA1����7�̊ԁA�܂�6��4��������_�ɂȂ�̂��킩��܂��B
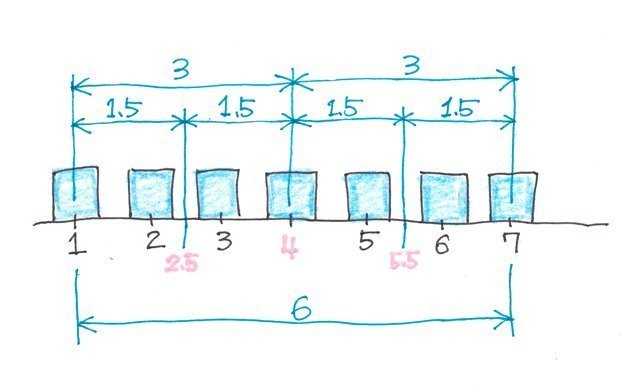
q1=1+1.5=2.5
q2=2.5�{1.5=4
q3=4+1.5=5.5
�ƂȂ�킯�ł��B�B�B
���āA����8�̃f�[�^��
�P�A�Q�A�V�A�P�O�A�P�P�A�P�T�A�P�W�Ƃ���ƁA
�܂�Q1��2.5�Ԗڂ̒l�ł����A2�Ԗڂ̃f�[�^��"2"�A3�Ԗڂ̃f�[�^��"7"�Ȃ̂�
Q1=2�{(7-2)��0.5��4.5
Q2��4�Ԗڂ̒l�́A�����_�͕t���Ȃ��̂ł��̂܂�
Q2=10
Q3��5.5�Ԗڂ̒l�́A5�Ԗڂ̃f�[�^��"11"�A6�Ԗڂ̃f�[�^��"15"�Ȃ̂�
Q3=11+(15-11)��0.5��13
�ƂȂ�܂��B
���ꂪ�AExcel��"QUARTILE��"�ł̓����_�i���̒����̕����j��p�����l���ʐ��i�_�j�̋��ߕ��ɂȂ�܂��B
���āA��ʓI�ɒm���Ă��鍂�Z��"���w�T"�ŋ������Ă�����@�͓����_�p������@�Ƃ͈قȂ��Ă��܂��B�ȒP�ɐ������Ă����܂��傤�B�B
���Z ���w�T�ŋ����l���ʐ��i�_�j���Z�̐��w�T�ŋ������Ă���l���ʐ��i�_�j�̒�`�͂����ł��B
��1�l���ʐ��F�ŏ��l���璆���l��1�O�܂ł̒l�̒����l
��2�l���ʐ��F�����l
��3�l���ʐ��F�����l�̌ォ��ő�l�܂ł̒l�̒����l
�ƂȂ�܂��B
�f�[�^�̌��������̏ꍇ�i8�j
������A�}�ɂ��Ă݂�ƁA
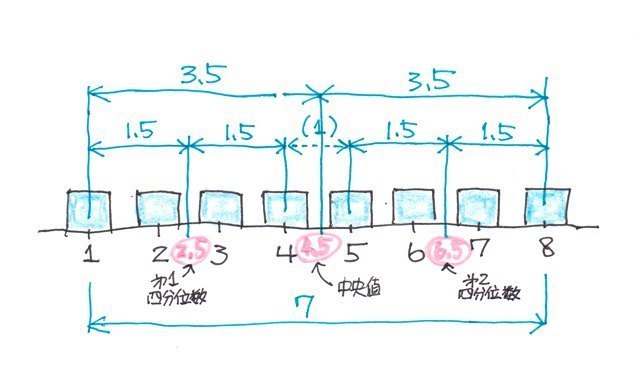
q1=1+1.5=2.5
q2=1+3.5=4.5
q3=8-1.5=6.5
�ƂȂ�܂��B
�ŁA����8�̃f�[�^���������P�A�Q�A�V�A�P�O�A�P�P�A�P�T�A�P�W�A�Q�O�Ƃ���ƁA
Q1=2+(7-2)x0.5=4.5
Q2=10+(11-10)x0.5=10.5
Q3=15+(18-15)x0.5=16.5
�ƂȂ��āAExcel�ł̒l�Ƃ͈قȂ鎖���킩��܂��B
�f�[�^�̌�����̏ꍇ�i7�j
�}�ɂ��Ă݂�ƁA
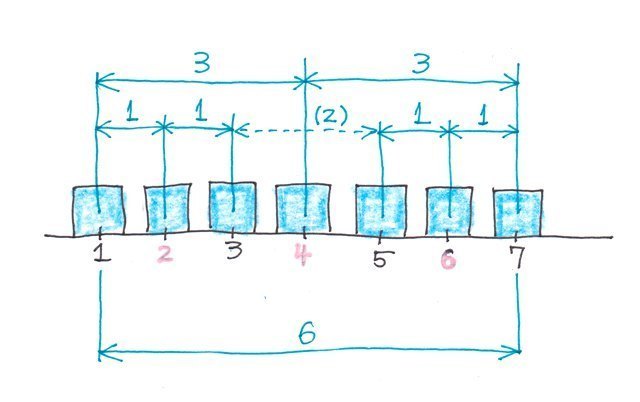
q1=1+1=2
q2=1+3=4
q3=7-1=6
�ƂȂ�܂��B
�ŁA����7�̃f�[�^���������P�A�Q�A�V�A�P�O�A�P�P�A�P�T�A�P�W�Ƃ���ƁA
Q1=2
Q2=10
Q3=15
�ƂȂ�܂��B
���AQUARTILE���Ŏ��ۂɒl�����߂Ă݂܂����̂ł������������B�l���ʔ͈͂Ƃ��l���ʔ͈͂ƌ����̂͑�R�l���ʐ��i�_�j�����P�l���ʐ��i�_�j���������l�ł��B
�܂��Q�l���ʐ��i�_�j�i�����l�j������50%�̃f�[�^�̐��͈̔͂ƌ������ƂɂȂ�܂��B
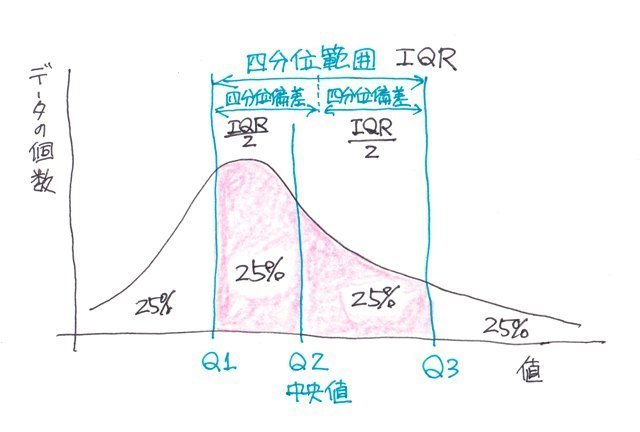 �l���ʕ��Ƃ�
�l���ʕ��Ƃ��l���ʔ͈͂�2�Ŋ������l�ŁA�����l�Ƌ��ɂ�����\����l�ɂȂ�܂��B
�A���A�l���ʐ��i�_�j�̓f�[�^�̌��ł̕����Ȃ̂ŁA��R�l���ʐ��i�_�j�|�����l�ƁA�����l�|��P�l���ʐ��i�_�j�͈�v����킯�ł͂���܂���B
�܂��A�W�����Ƃ͈���āA���Ƃ��ƍ��E�Ώ̂̐��K���z�ł͂Ȃ����z�ɑ����\�l�Ȃ̂ŁA�����l�}�l���ʕ��ƌ����������͓K���ł͂���܂���B
�Ȃ̂ŁA�ނ���l���ʔ͈͂����������ǂ��Ǝv���܂��B�B
�O��l�Ɠ��ٓ_�̖ڈ��O��l�̖ڈ��Ƃ��Ĉ�ʓI��
�O��l<��1�l���ʐ�-1.5x�l���ʔ͈�
�O��l>��3�l���ʐ�+1.5x�l���ʔ͈�
�Ƃ���Ă���B
�܂��A�X�ɂ�����O��Ă���f�[�^�̎���"���ٓ_"�Ƃ�����
���ٓ_<��1�l���ʐ�-3x�l���ʔ͈�
���ٓ_>��3�l���ʐ�+3x�l���ʔ͈�
�Ƃ���Ă��܂��B
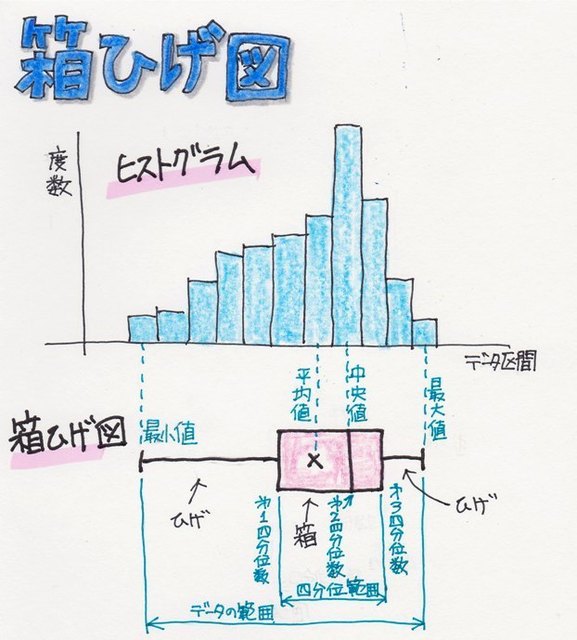
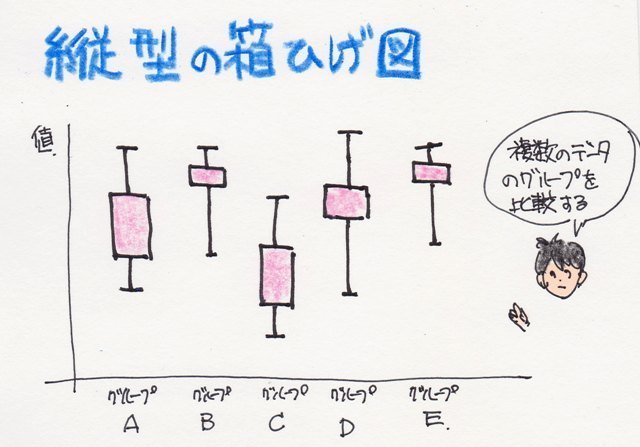
���Ђ��}���ꂩ��A�l���ʐ��i�_�j��}�ɂ����̂�"���Ђ��}"�Ƃ����܂��B
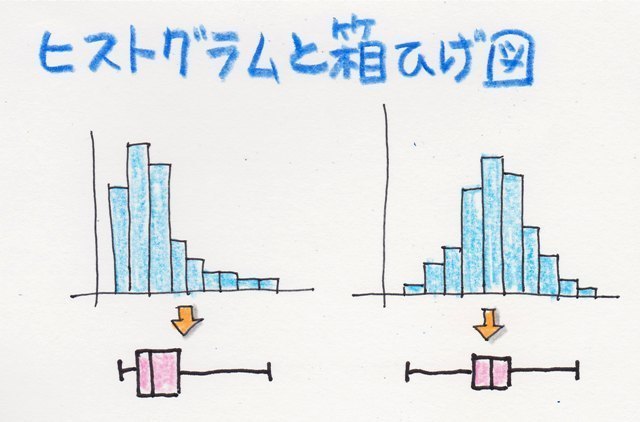
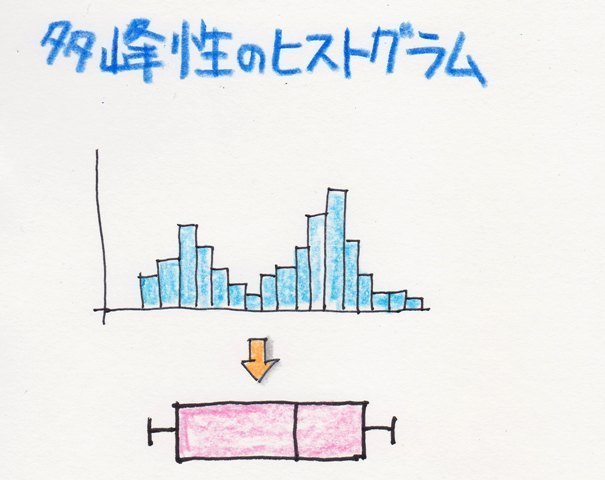
���Ђ��}��`���Ƃ��������q�X�g�O������`���Ȃ��Ă��f�[�^�̕��z�̗l�q��������x������悤�ɂȂ�܂��B
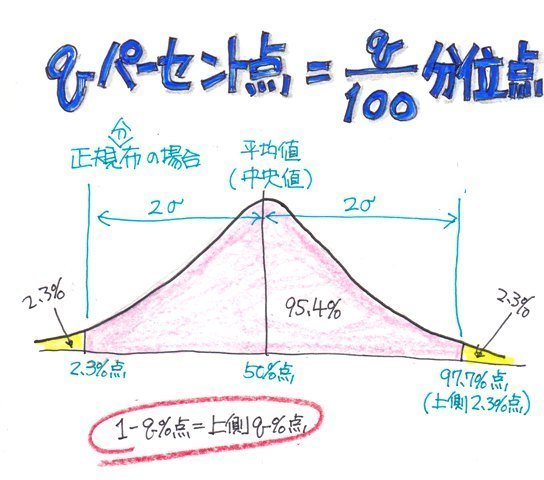
�ڂ����̓R�`�������Ă��������B���āA����͎l���ʐ��i�_�j�ł͂Ȃ����R�ȁ������ʐ��i�_�j�ŕ]������p�[�Z���g�_�ɂ��ĉ�����܂��B
 �o�b�N�i���o�[1�D���ϒl�Ƒ�\�l�i�����l�j2�D�Z�p���ρi�������ρj�Ɖ��d���ς̈Ⴂ�́H�u�d�݁v���ăi�j�I�H 3�D�����l�ɂ��Ă܂Ƃ߂Ă݂��i���ϒl�Ɖ����������H�j�֘A�y�[�WQUARTILE���Ŏl���ʓ_�����߂Ă݂����v���͂̊�{���̊�{�A�x�����z�\�ɂ��Ă܂Ƃ߂Ă݂����l�f�[�^�̕��z���݂�q�X�g�O�����ɂ��Ă܂Ƃ߂Ă݂����K���z�ɂ��������l�����߂�MEDIAN���f�[�^���͂̉��/���j���[
�o�b�N�i���o�[1�D���ϒl�Ƒ�\�l�i�����l�j2�D�Z�p���ρi�������ρj�Ɖ��d���ς̈Ⴂ�́H�u�d�݁v���ăi�j�I�H 3�D�����l�ɂ��Ă܂Ƃ߂Ă݂��i���ϒl�Ɖ����������H�j�֘A�y�[�WQUARTILE���Ŏl���ʓ_�����߂Ă݂����v���͂̊�{���̊�{�A�x�����z�\�ɂ��Ă܂Ƃ߂Ă݂����l�f�[�^�̕��z���݂�q�X�g�O�����ɂ��Ă܂Ƃ߂Ă݂����K���z�ɂ��������l�����߂�MEDIAN���f�[�^���͂̉��/���j���[