
回帰分析というのは今までのデータを分析して将来(未知)の状況を予測すること。
例えば、気温とソフトクリームの販売数のデータから今まで経験したことのない猛暑日の気温の時のソフトクリームの販売数を予測することです。
そして「回帰」というのは、「気温」と「ソフトクリームの販売数量」の間に数式(y=f(x))を設定することです。
ここで、設定した数式によって予測する「ソフトクリームの販売数量」が“y”「従属変数(目的変数)」
「ソフトクリームの販売数量」を予測するために計算に使用する「気温」を“x”「独立変数(説明変数)」と言います。
つまり、「ソフトクリームの販売数量」を予測したいために「気温」から予測できるのではないかと目を付けて過去のデータを分析して数式を当てはめたということです。
これが、「回帰分析」です。
なんか、説明がくどかったように思うのですが、、、
何故か、それは2つのデータの間の関係は「相関関係」というのがあって、相関係数などでその関係を分析することができるんですが、一見似たような感じがしますが、「相関関係」の分析と「回帰分析」はごっちゃにしないではっきりと分けて考えていなければなりません。
相関関係に関しては、相関係数や、散布図で確認することなどについて載せていますので是非見ておいてください。
簡単に言うと(?)「相関関係」の分析は2つのデータの関係性を分析することですが、回帰分析とは関係性を設定した上であくまでもデータを予測することを目的にしています。
なので、回帰分析の結果が同じでも、それぞれの相関関係がちがっていると回帰分析によって求めた予測値が当たる確率が違ってきたりしてしまいます。
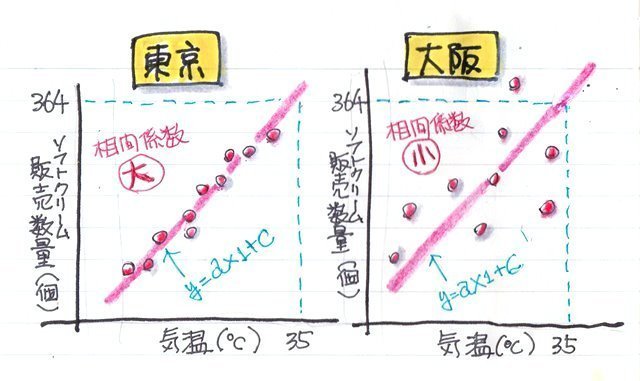
この時、この2つのデータは販売した場所が東京と大阪と違っています。では何の影響で「気温」と「ソフトクリームの販売数量」の相関関係が変わってきたのでしょうか?
それは、相関関係を分析して調べていかなければなりません。
たまたま、このソフトクリーム販売店のオーナーは東京と大阪の販売店のデータを分けて分析していたので、この違いに気が付くことができましたが、もし一緒にしてデータを収集していたらその違いに気づかずに回帰分析をして来るべき猛暑日の販売数量を予測して仕込んでいたら外れてしまってたかもしれませんよね。
なので、順番としては相関関係の分析を行ってから回帰分析をするのが間違いが少なくなるのだと思います。
さて、話を戻して。。。
この「ソフトクリームの販売数量」の様に「気温」1つだけで予測するのを「単回帰分析」
実はこのソフトクリーム屋はイベントに出店している屋台で、イベントの来場者数によっても販売数量が変わってしまうように、「気温」と「イベントの来場者数」の様に2以上の独立変数で予測するのを「重回帰分析」と言います。
式で書くと
単回帰分析は
y=ax1+c
y:ソフトクリームの販売数量
x1:気温
a,c:係数(パラメータ)
ExcelのFORECAST関数を使って気温が35℃の時のソフトクリームの販売数量を予想してみましょう。
重回帰分析は
y=ax1+bx2+c
x2:イベントの来場者数
b:係数(パラメータ)
今度はExcelのTREND関数を使って、気温35℃でイベント来場者数が1万人の時のソフトクリームの販売数量を予想してみましょう。
このパラメータ、a、b、cは近似直線と実際の各データの誤差の二乗が最小になる様に最小二乗法で求めます。
今日はここまで! (^_-)-☆
関連ページ
・独立変数(説明変数)と従属変数(目的変数)
・其の1 相関関係についてまとめてみた
・其の2 相関関係で気をつけたいこと(散布図を画いて確認しよう!)
・其の3 散布図についてまとめてみた(どっちが横軸?)
・其の4 相関関係と因果関係、疑似相関と潜在変数についてまとめてみた
・其の4.1 散布図を画いてみた / グラフ
・FORECAST関数で値(例えば販売数量とか)を予想してみた
・TREND関数で値(例えば販売数量とか)を予想してみた
・COVAR関数で共分散を求めてみた
・CORREL関数で相関係数を求めてみた
・データ分析の解説/メニュー
ラベル:回帰分析

