今回は「幾何平均(相乗平均)」についてまとめてみます。
例えば、会社の売り上げが2014年は前年(2013年)の5%アップ(1.05倍)、2015年は前年(2014年)の10%アップ(1.1倍)でした(好調ですね!)
この時、2014年と2015年の2年間の平均アップ率は何%か?
これを、単に算術平均で、
(1.05+1.1)÷2=1.075(7.5%アップ)
でいいかと言うと。。。?
実際に計算してみましょう。
2013年の売上を100万円としてみましょう。
2014年は5%アップなので、
1,000,000円x1.05=1,050,000円
2015年はその10%アップなので、
1,050,000円x1.1=1,155,000円になります。
では、算術平均で求めた年平均7.5%で計算してみると?
2014年は、
1,000,000円x1.075=1,075,000円
2015年は、
1075,000円x1.075=1,155,625円
になってしまいました。間違いですね!
とこのような時に幾何平均(相乗平均)Geometric Meanを用います。
幾何平均とは、掛け算の積の平均のことで、算術平均の時は足し算の平均で足し算の和を値の数nで割りましたが、幾何平均は掛け算の積を累乗根(n乗根)します。
式で書くとこうなります。

先ほどの例題を解いてみると、
√(1.05x1.1)=1.07470926301(かなり細かいですが。。。(*_*;)
2014年は、
1,000,000円x1.07470926301=1,0747,092.6301円
2015年は、
1,0747,092.6301円x1.07470926301=1,155,000円
になりました!
幾何学的に解説すると、2つの値の幾何平均は同じ面積の正方形の1辺、3つの値の幾何平均は同じ体積の立方体の1辺の長さを求めることと同じになります。
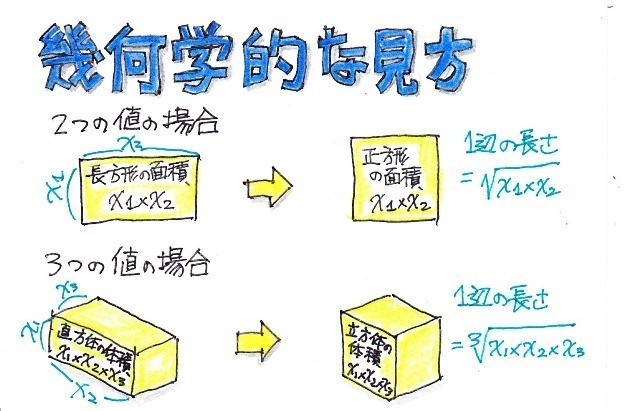
こうしてみると、これが平均になることが理解しやすくなりますね。
次回は、3つ目の平均、調和平均についてまとめてみましょう!
バックナンバー
1.平均値と代表値(特性値)
関連ページ
算術平均(相加平均)と加重平均の違いは?「重み」ってナニ!?
中央値(median / メジアン)についてまとめてみた
データ分析の解説/メニュー

