値の総和(合計)を値の個数で割った値のことを言います。
例えば、5人のテストの点数が
40点、50点、70点、80点、60点の時の平均は
(40+50+70+80+60)=300
300÷5=60
60点になります。

で、この平均値はそれぞれの点数との差、つまり「距離」が平均値の左側の距離の合計と右側の距離の合計が同じになる、つまり釣り合う「重心」と言うことができます。
この場合、左側、右側の距離の合計は10+20=30で釣り合っています。
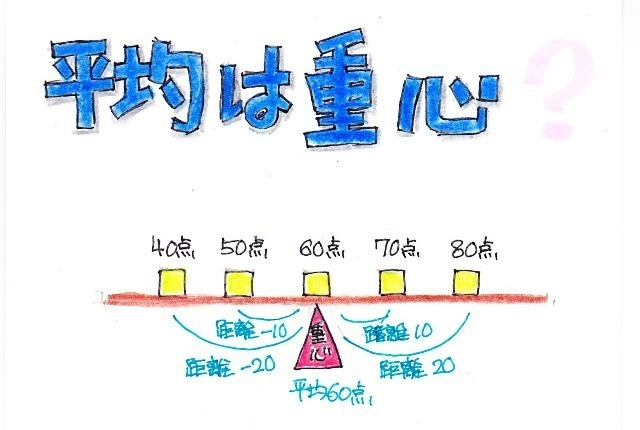
この釣り合いの天秤をイメージする時、間違えてはいけないことは、天秤の長さ(横軸)は値、つまりここでは点数です。天秤に乗っている錘の重さが点数なのではありません。錘は値(点数)の個数です。ここでは、それぞれ1個です。
数式で書くと算術平均は

釣り合いの式は、平均値の左側はマイナス、右側はプラスになるので合計が0(左右が釣り合う)になります。

加重平均
では、加重平均とは何かというと、、
一般的にこんな説明をよくみかけます。
「それぞれの値に重みがある場合、その重みを付けて求めた平均値」。。。
例えば、5人のテストの点数が、
40点が3人、90点が2人の時、各点数をとった人数("3"と"2")を「重み(ウェイト:w)」として、
加重平均は
40x3+90x2=300
300÷(3+2)=60
60点となります。

と言う説明が一般的にされています。
元々「平均」と言うのは、
「値の総和を値の個数で割った値」ですから、この加重平均って算術平均と何が違うの?
(40+40+40+90+90)÷5=60を
(40x3+90x2)÷(3+2)
って書き換えただけじゃないの?って思う。「重み」って何だ!?と単純に疑問が湧く。
あと、こんな説明
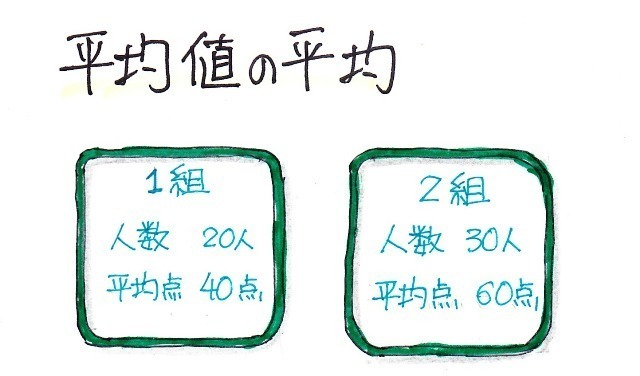
1学年で2つのクラスがあってテストの結果、
1組の平均値が40点、2組の平均値が60点だった時、この学年のテストの平均値は?という例題、
比較的これは「重み」の意味が理解しやすい例題です。
算術平均では、
(40+60)÷2=50?
これは学年のクラスの平均値ですよね。分母の"2"はクラスの数ですから、、
では、「この学年のテストの平均値」と言う問いは何を求めたいか?
生徒1人当たりの平均値ですよね、普通。
すると、「値の総和を値の個数で割る」のだから、各組の生徒の人数を加味しなければなりません。
1組の生徒の数は20人、2組は30人なので、
値の総和は、40x20+60x30=2600点
値の個数は、20+30=50人
で、生徒1人当たりのテストの平均値は
2600÷50=52点 になります。
この場合、各クラスの生徒数を「重み」として
加重平均は、(40x20+60+30)÷(20+30)=52
となります。
式で書くとこうなります。

算術平均と加重平均の違いは?
んで、根本的に算術平均と加重平均の違いは何かと言うと、、、
同じなんです!
加重平均の重みが全て"1"の特殊なケースが算術平均と言うわけなんです。
最初の例題、5人のテストの算術平均の式は、実はそれぞれの重み"1"が省略されているだけなんです。
つまり、
40点が1人、50点が1人、70点が1人、80点が1人、60点が1人の時の加重平均は
(40x1+50x1+70x1+80x1+60x1)÷(1+1+1+1+1)=300÷5=60
と言うわけです。
んで、算術平均は平均値の左側と右側の距離が釣り合う「重心」という説明をしましたが、
加重平均の「重み」とは正に天秤に置く「錘(おもり)」そのものなんです。
中学の理科で習う「力の釣り合い」や「重心」の計算そのもの。
高校物理では「モーメント」として定義されます。
「腕の長さとその錘の重さの積が釣り合う場所が重心」その「重心」が「加重平均」
「錘の重さ」こそが加重平均でいう「重み」になるわけです。
最初の加重平均の例題の
「5人のテストに点数が、40点が3人、90点が2人の時」というのは、言い換えると
40点の位置に錘が3つ、90点の位置に錘が2つある時の重心位置はどこか?になります。
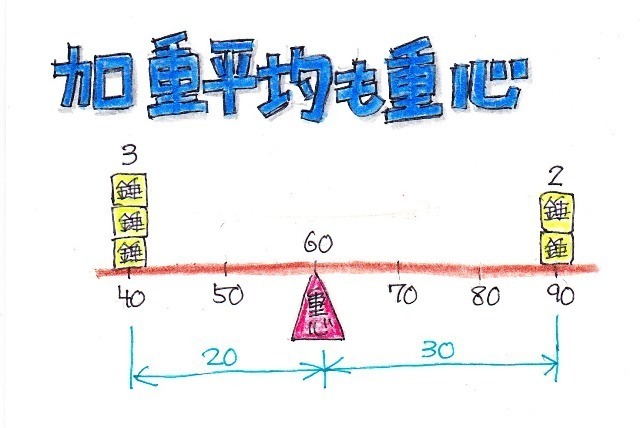
ちなみに、物理の重心位置を求める式は、

加重平均の式と同じです。
んで、これって数学の内分点の式なんです。
線分A、Bがあって点Pがm:nの位置にある時に「点Pは線分A、Bをm:nに内分する」と言い
内分点の位置はこのように求められます。
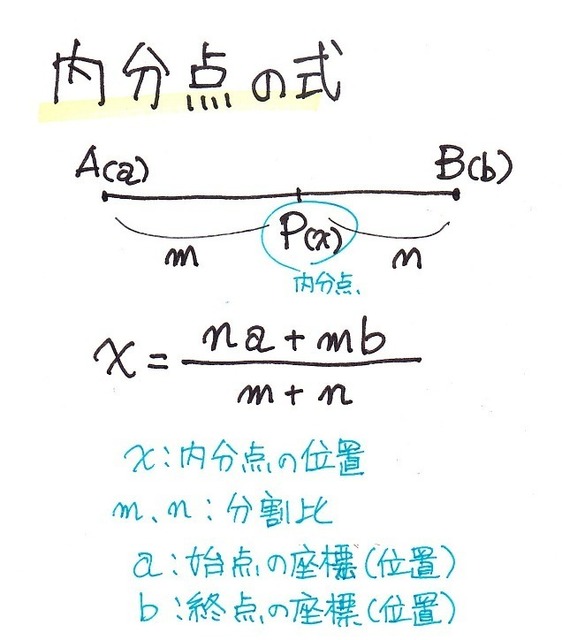
これまた、加重平均の式と同じです。
ところで、この内分点は「四分位数」(データ分布のばらつきを表す指標)を求める時も登場します。
ところで、Excelでは加重平均を直接求める関数はないのですが、配列の積(掛け算)の合計を求める「SUMPRODUCT関数」と言うのがあり、いわゆる"重み付けの合計"を求めることができます。この結果を重みの合計で割れば加重平均を算出することが可能です。
さて「平均」と言うのは「値を足して個数で割る」算術平均だけではありません、掛け算をしたり逆数を足したり、色々な平均があります。それらを良く理解していないと、なんでもかんでも算術平均で平均が求められると勘違いしてしまいます。
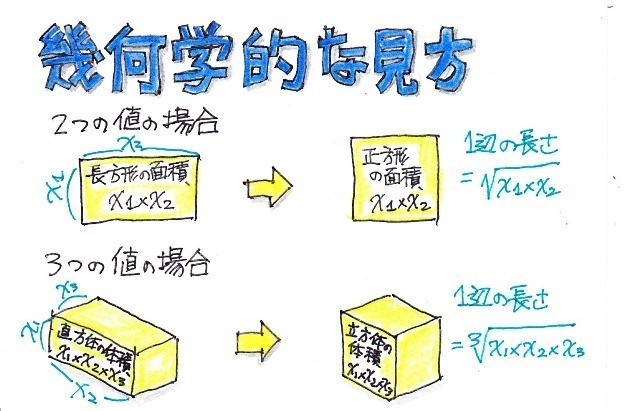
次回はそんな色々な平均の1つ「幾何平均(相乗平均)」についてみてみましょう!
バックナンバー
1.平均値と代表値(特性値)
関連ページ
配列の掛け算の合計を求るSUMPRODUCT関数で加重平均を求めてみた
QUARTILE関数で四分位点を求めてみた
統計分析の基本中の基本、度数分布表についてまとめてみた
数値データの分布をみるヒストグラムについてまとめてみた
正規分布について
中央値を求めるMEDIAN関数
データ分析の解説/メニュー

