ばらつきの代表値"標準偏差"も平均値と同じく集団のデータ分布が正規分布に近い場合に有効な値になります。と言うのも、標準偏差も平均値とデータの差をばらつきとしているためです。
そこで、データの分布が正規分布でないような場合でも簡単にばらつきの状態を評価するのが、"四分位数(Quartile)"または"四分位点(Quartile point)"、"四分位範囲(Interquartile range / IQR)"、"四分位偏差(Quartile deviation)"になります。
なので、中央値を代表値とする場合は、ばらつきは四分位偏差を代表値とします。
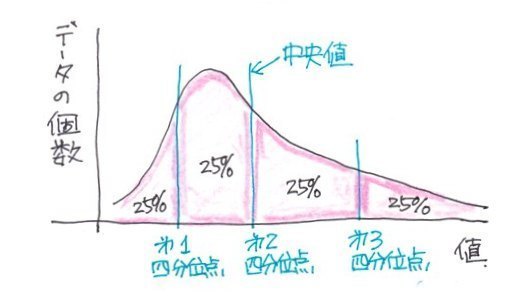
四分位数はデータを最小値から最大値まで順に並べて4分割(25%ずつ)した時、
第1四分位数(Q1):25%の値
第2四分位数(Q2):50%の値(中央値)
第3四分位数(Q3):75%の値
とします。
四分位数(点)の求め方
四分位数(点)の求め方は実は色々あるのですが、このサイトはExcelを実行手段としたサイトなのでExcelのQUARTILE関数をベースとした求め方で説明します。
内分点(線の長さの分割)を求める方法を使用しています。
これは、高校の数学Ⅰで教えられている四分位数とは異なります。数学Ⅰの四分位数は後ほど説明いたします。。
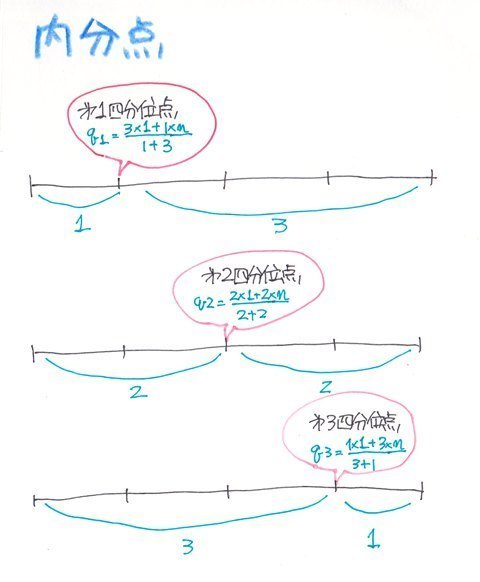
内分点と言うのは全体(データの個数:n)をa:bに分割する時、その分割点qは
q=(bx1+axn)/(a+b)
で求められます。
つまり四分位数の場合は全体を4分割するので、第1四分位点q1は1:3に分割する点、第2四分位点は2:2に分割する点、第3四分位点は3:1に分割する点ということになります。
データの個数が偶数の場合
データの数を8個の場合を求めてみます。
第1四分位数(点)はデータの個数を1:3に分割する内分点になるので
q1=(3x1+1x8)/(1+3)=2.75
最小値から2.75番目のデータ
第2四分位数(点)はデータの個数を2:2に分割する内分点なので
q2=(2x1+2x8)/(2+2)=4.5
最小値から4.5番目のデータ
第3四分位数(点)はデータの個数を3:1に分割する内分点なので
q3=(1x1+3x8)/(3+1)=6.25
最小値から6.25番目のデータ
となります。
分かりやすく図にしてみると、1から8の間、つまり7を4等分する点となるのがわかります。
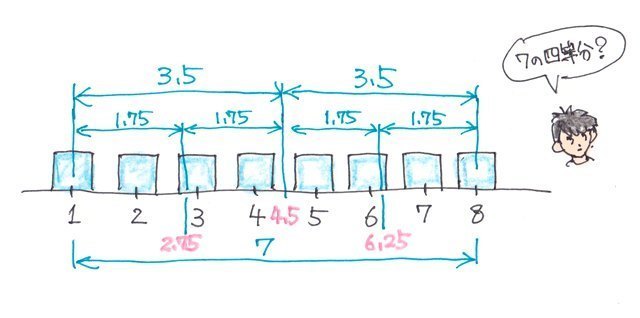
q1=1+1.75=2.75
q2=2.75+1.75=4.5
q3=4.5+1.75=6.25
となるわけです。。。
さて、この8つのデータが
1、2、7、10、11、15、18、20とすると、
まずQ1の2.75番目の値ですが、2番目のデータが"2"、3番目のデータが"7"なので
Q1=2+(7-2)x0.75=5.75
Q2の4.5番目の値は、4番目のデータが"10"、5番目のデータが"11"なので
Q2=10+(11-10)x0.5=10.5
Q3の6.25番目の値は、6番目のデータが"15"、7番目のデータが"18"なので
Q3=15+(18-15)x0.25=15.75
となります。
データの個数が奇数の場合
今度はデータの個数が奇数の7個の場合です。
第1四分位数(点)はデータの個数を1:3に分割する内分点になるので
q1=(3x1+1x7)/(1+3)=2.5
最小値から2.5番目のデータ
第2四分位数(点)はデータの個数を2:2に分割する内分点なので
q2=(2x1+2x7)/(2+2)=4
最小値から4番目のデータ
第3四分位数(点)はデータの個数を3:1に分割する内分点なので
q3=(1x1+3x7)/(3+1)=6.25
最小値から5.5番目のデータ
となります。
分かりやすく図にしてみると、1から7の間、つまり6を4等分する点になるのがわかります。
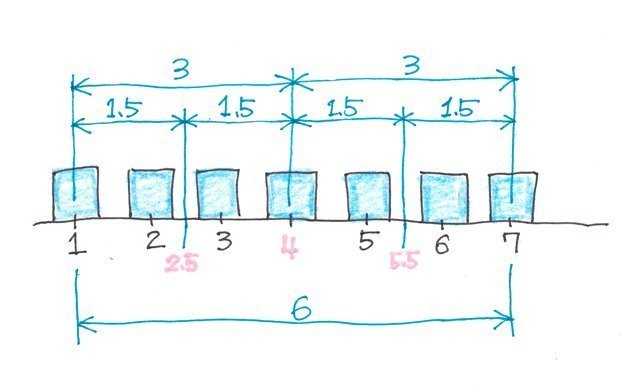
q1=1+1.5=2.5
q2=2.5+1.5=4
q3=4+1.5=5.5
となるわけです。。。
さて、この8つのデータが
1、2、7、10、11、15、18とすると、
まずQ1の2.5番目の値ですが、2番目のデータが"2"、3番目のデータが"7"なので
Q1=2+(7-2)x0.5=4.5
Q2の4番目の値は、小数点は付かないのでそのまま
Q2=10
Q3の5.5番目の値は、5番目のデータが"11"、6番目のデータが"15"なので
Q3=11+(15-11)x0.5=13
となります。
これが、Excelの"QUARTILE関数"での内分点(線の長さの分割)を用いた四分位数(点)の求め方になります。
さて、一般的に知られている高校の"数学Ⅰ"で教えられている方法は内分点用いる方法とは異なっています。簡単に説明しておきましょう。。
高校 数学Ⅰで教わる四分位数(点)
高校の数学Ⅰで教えられている四分位数(点)の定義はこうです。
第1四分位数:最小値から中央値の1つ前までの値の中央値
第2四分位数:中央値
第3四分位数:中央値の後から最大値までの値の中央値
となります。
データの個数が偶数の場合(8個)
これも、図にしてみると、
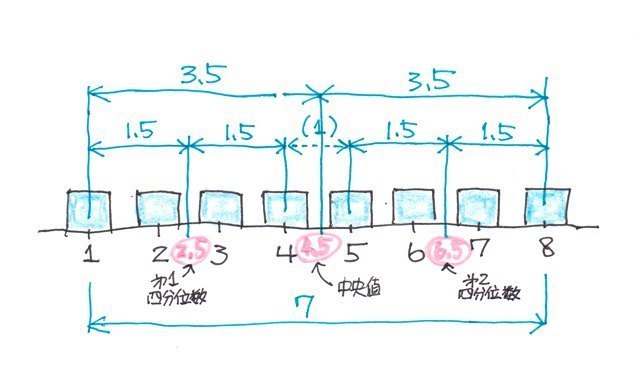
q1=1+1.5=2.5
q2=1+3.5=4.5
q3=8-1.5=6.5
となります。
で、この8個のデータが同じく1、2、7、10、11、15、18、20とすると、
Q1=2+(7-2)x0.5=4.5
Q2=10+(11-10)x0.5=10.5
Q3=15+(18-15)x0.5=16.5
となって、Excelでの値とは異なる事がわかります。
データの個数が奇数の場合(7個)
図にしてみると、
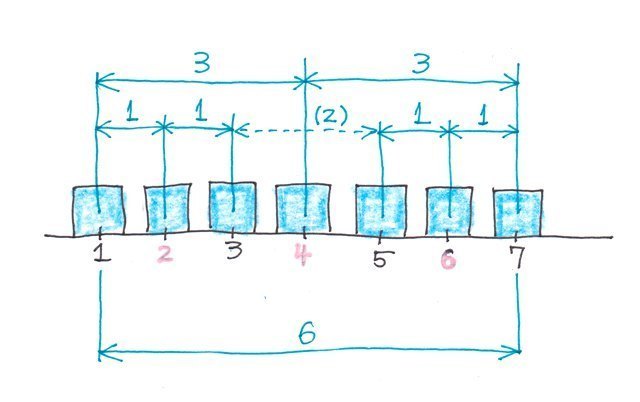
q1=1+1=2
q2=1+3=4
q3=7-1=6
となります。
で、この7個のデータが同じく1、2、7、10、11、15、18とすると、
Q1=2
Q2=10
Q3=15
となります。
尚、QUARTILE関数で実際に値を求めてみましたのでご覧ください。
四分位範囲とは
四分位範囲と言うのは第3四分位数(点)から第1四分位数(点)を引いた値です。
つまり第2四分位数(点)(中央値)を挟んだ50%のデータの数の範囲と言うことになります。
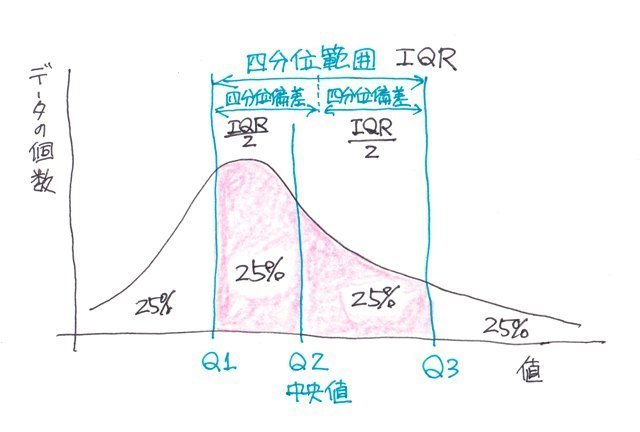
四分位偏差とは
四分位範囲を2で割った値で、中央値と共にばらつきを代表する値になります。
但し、四分位数(点)はデータの個数での分割なので、第3四分位数(点)−中央値と、中央値−第1四分位数(点)は一致するわけではありません。
また、標準偏差とは違って、もともと左右対称の正規分布ではない分布に対する代表値なので、中央値±四分位偏差と言う捉え方は適当ではありません。
なので、むしろ四分位範囲を見た方が良いと思います。。
外れ値と特異点の目安
外れ値の目安として一般的に
外れ値<第1四分位数-1.5x四分位範囲
外れ値>第3四分位数+1.5x四分位範囲
とされている。
また、更にそれより外れているデータの事を"特異点"といって
特異点<第1四分位数-3x四分位範囲
特異点>第3四分位数+3x四分位範囲
とされています。
箱ひげ図
それから、四分位数(点)を図にしたのを"箱ひげ図"といいます。
箱ひげ図を描くといちいちヒストグラムを描かなくてもデータの分布の様子がある程度分かるようになります。詳しくはコチラを見てください。
さて、次回は四分位数(点)ではなく自由な○○分位数(点)で評価するパーセント点について解説します。
バックナンバー
1.平均値と代表値(特性値)
2.算術平均(相加平均)と加重平均の違いは?「重み」ってナニ!?
3.中央値についてまとめてみた(平均値と何がちがう?)
関連ページ
QUARTILE関数で四分位点を求めてみた
統計分析の基本中の基本、度数分布表についてまとめてみた
数値データの分布をみるヒストグラムについてまとめてみた
正規分布について
中央値を求めるMEDIAN関数
データ分析の解説/メニュー

