今回はその準備として"標本空間"と"事象"という用語についてまとめてみました。
数学的な確率の定義になると"集合"と同じような考え方が登場し、集合で使われた記号なんかも登場してきます。。。
標本空間について
標本空間(Sample space)というのは、試行によって起きうるすべての結果(根元事象)を含む集合のことを言います。
と、いうと分かり辛いですよねー。。。
いきなり"集合"なんてのが出てくるし。。
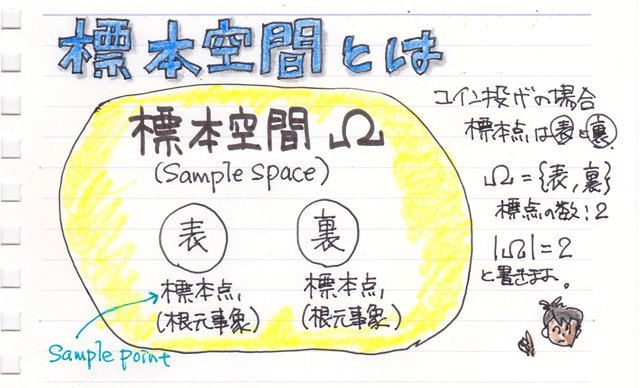
例えば、コイン投げの場合、結果の{表}と{裏}を"標本点"(Sample point)と言います。つまり前回の"根元事象"のことです。
で、この標本点を含む集合(全体)を"標本空間"と言います。
サイコロ振りの場合は{1}、{2}、{3}、{4}、{5}、{6}の標本点(根元事象)を含む集合のことになります。
記号は"Ω"で表します。
事象について
前回も事象の説明はしてありますが、数学的にいうと、
事象(Event)というのは標本空間(Ω)の中で全ての起きうること。
標本空間の部分集合になります。
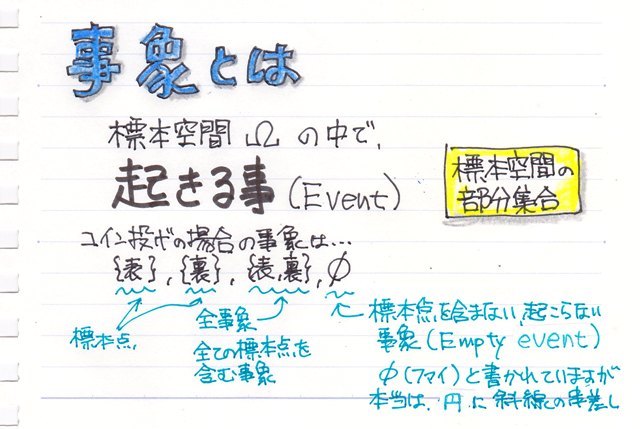
コイン投げの場合だと、標本点(根元事象)の{表}、{裏}の他に{表、裏}(表か裏がでる事象)、∅(空事象)も含まれます。
"∅"は空事象と言って、標本点をなにも含まない事象、つまり何も起こらない事象のことを言います。
さて次回は、事象の組合せについてまとめてみました。
バックナンバー
其の1 確率についてまとめてみた
関連ページ
データ分析の解説/メニュー

