っていうのを相関関係があるといいます。
ドラマやなんかの登場人物の関係も“相関図”と言ったりしますが、それはちと意味が違います。
相関関係を調べるデータは基本的に最終的には連続した数値データにするのが分析には適していると思います。
分かりやすい例をあげると、、
季節(月)と電気料金の関係だったら、気温と電気料金とか
子供の算数の成績(テストの点数)と理科の成績とか、
スーパーでの気温と、ビールの販売数とか。。。
など、大体想像がつきそうなデータの関係だけではなくて、2つのデータがどんな関係があるか、どのデータを対象にした方が関係性が強いかを分析することも重要です。
例えば、気温とビールの販売数の関係は、気温より湿度のデータの方がより関係があったりとか?(ないか。。?)
算数と、理科の成績の相関?
理系と文系の教科の場合、理系の方が塾に通っている子供が多いとしたら。。。
塾に通ってる子と算数または理科の成績の相関ってことになるかも!?
つまり、そこがデータ分析の肝になるところ。。色んな角度でデータを集めて分析することが必要なことになる。。
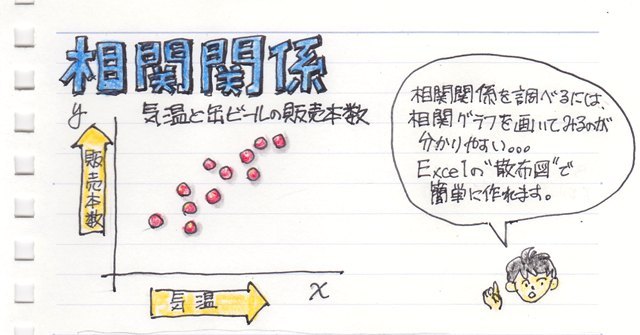
相関関係を見る相関グラフ(散布図)
2つのデータの相関関係を調べるには、まず相関グラフを画いてしまうのが手っ取り早く全体の傾向をつかむのに有効です。
具体的には、2つのデータを横軸と縦軸にとった“散布図”を画きます。
数学的にいうと“x-yグラフ”になります。ちなみに横軸が“x”、縦軸が“y”になります。
Excelを使うと散布図を簡単に画くことが出来ます。
散布図については後ほどまとめておきます。。
相関係数
話が逸れてしまったけど、
相関グラフを画いてみて分かることはばらつきの大小と、グラフの傾向、右肩上がりか右肩下がりか、それと直線ではなく曲線的な傾向があるかないか等など。。
んで、相関グラフでの特性を表す値(特性値)に“相関係数”というのがあります。
ばらつきが無く一直線上にある場合は“1”、ばらつきが大きく右肩上がりか右肩下がりかグラフの傾向も分からないような場合は“0”になります。
また、右肩上がりはプラス(正の値)、右肩下がりはマイナス(負の値)になります。
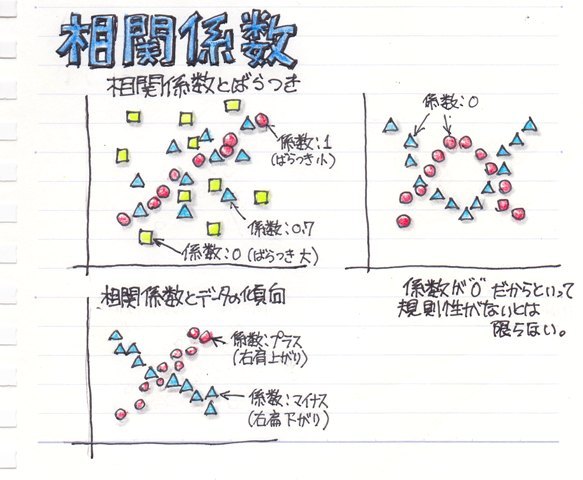
相関係数は2つのデータが直線的な傾向を判断する特性値なので、相関係数が“0”でもばらつきが大きい場合とは限らず、曲線的な規則性に当てはまっている場合もあります。
共分散と相関係数
さて、相関係数はどうやって計算するかというと。。。
まず“共分散”というのを求めます。
共分散は標準偏差を求める時の分散と同じような考え方で、“x”と“y”の平均との差をかけてその平均を求めます。
分散はその“x”だけ(または“y”だけ)の特殊なケースと言えるかもしれません。
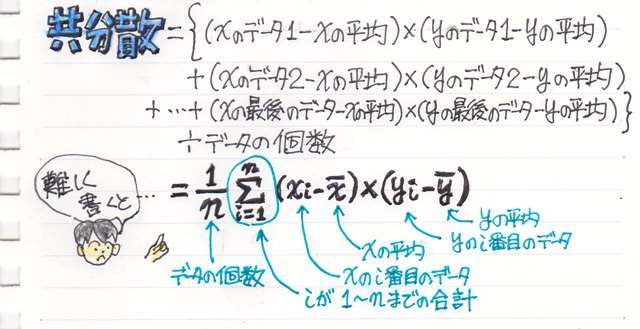
共分散を求めることで相関係数がプラス(右肩上がり)かマイナス(右肩下がり)かが分かります。
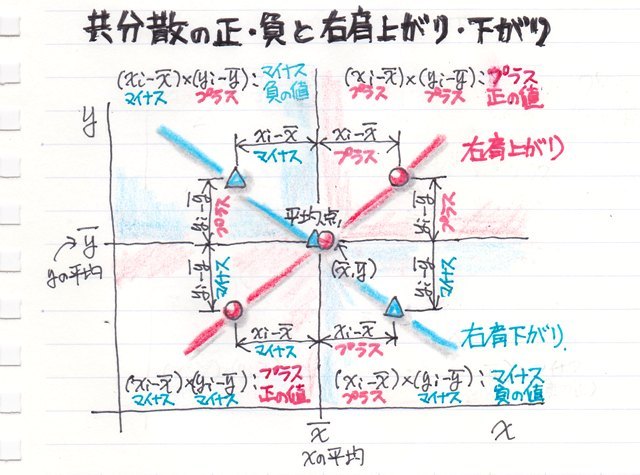
“x”と“y”の平均値の点から右上、左上、右下、左下の4つの範囲に分けると、
xの平均との差とyの平均との差の積(掛け算)がプラスになる範囲は、右上と左下の範囲になり、この範囲を通るグラフは右肩上がりになります。
逆に、xの平均との差とyの平均との差の積(掛け算)がマイナスになるのは左上と右下の範囲になり、個の範囲を通るグラフは右肩下がりになります。
共分散の値の単位はxの単位とyの単位の積になります。
例えば、気温とビールの販売数の共分散だったら、単位は“℃・本”になります。
またその値も、ビールを販売する店によって販売量が異なると共分散の値も変わってくるでしょう。
そこで、相関係数を使って、いろいろな相関関係の特性を共通の値で表すわけです。。
ちなみに、共分散はExcelの“CONVAR関数”で簡単に求めることができます。

相関係数の単位は共分散をxの単位を持つxの標準偏差と、yの単位を持つyの標準偏差で割るため単位が無くなります(無次元)。
また、相関係数の値は“-1〜1”の範囲の値になります。
相関係数と、相関関係の相関の強さの目安は、
相関係数>0.7:相関が強い
0.4<相関係数<0.7:相関が中間的(な強さ)
0.2<相関係数<0.4:相関が弱い
相関係数<0.2:相関が見られない
とされています。
(目安なので“以上”、“以下”かどうか細かいことは気にしないでくださいね!)
また、相関係数はExcelの“CORREL関数”で簡単に求めることができます。
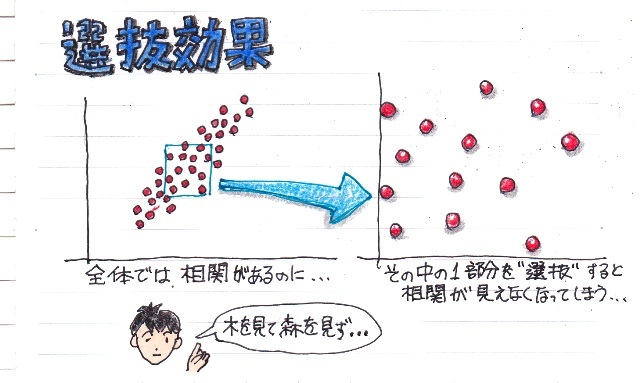
と、相関係数さえ求めれば、相関関係が分かってしまうように思いますが実際は、そう単純な話ではありません。
次は、相関関係を調べる時の注意しなければならないことについてまとめてみました。
予告編
関連ページ
其の2 相関関係で気をつけたいこと(散布図を画いて確認しよう!)
其の3 散布図についてまとめてみた(どっちが横軸?)
其の4.1 散布図を画いてみた / グラフ
COVAR関数で共分散を求めてみた
CORREL関数で相関係数を求めてみた”
データ分析の解説/メニュー

