正規分布(Normal Distribution)、ガウス分布ともいいます。
その前に、統計分析の基本、"度数分布"や"ヒストグラム"についてのおさらいはコチラをどうぞ!
正規分布の形
正規分布というのは“分布”の形のことなので、度数分布のグラフつまり“ヒストグラム”の形が平均値を中心に釣り鐘状に分布していることを言います。
どんなデータの分布が正規分布になるかと言うと、例えば、人の身長の分布(と言っても、年齢や性別を限定する必要があります)とか、サイコロをたくさん振った時の出目の分布とか、製造現場では何か部品を加工した時の寸法のバラつきの分布とか。。。
ある自然現象、社会現象のデータの分布にも多くあると言われます。
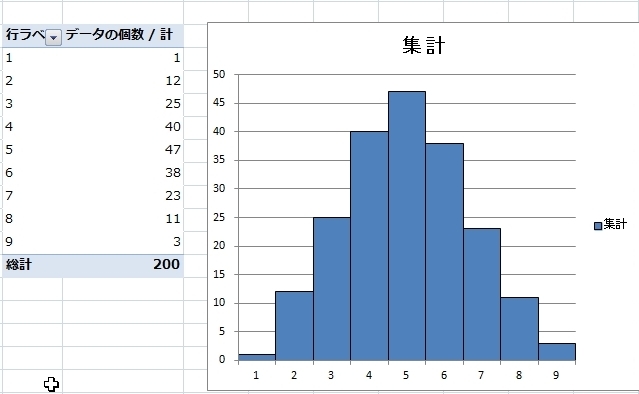
具体的にはこんな形の分布になります。
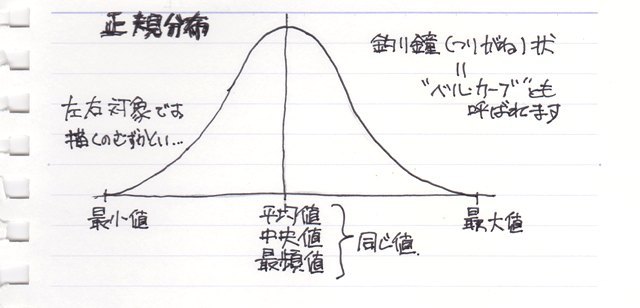
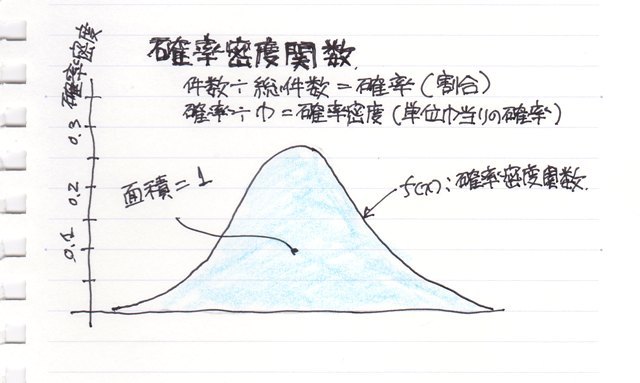
但し、正式な意味では、グラフの縦軸はヒストグラムの場合の個数や件数ではなく、確率になります。しかも“確率密度”つまりグラフの全体の面積を“1”とした、単位幅当たりの“確率”。。。
例えばヒストグラムの縦軸の度数(個数、件数)を総件数で割ったもの(20%とか、50%とか)を相対度数と言いますがそれが“確率”に当たります(なのでグラフの面積が"1"になります)、それを更に横軸の幅で割ったものが単位幅当たりの確率で“確率密度”になります。(つまり確率を微分したものです、、よけい分からない!?)
“確率”と言うと、いきなり難しそうなので、“割合”だと考え方を変えてしまいましょう。。。
Excelの統計関数では、“NORMDIST関数”で正規分布の“確率密度”、“累積分布”を求めることができ、そこから正規分布のグラフを画くこともできます。また後から登場する尖度(せんど)を求める“KURT関数”、歪度(わいど)を求める“SKEW関数”、等もあります。
確率密度関数
んで、そろそろ本題ですがその正規分布の形というのを数式で描くとこうなります

ここで、平均値“μ(みゅー)”ってのが出てくるんですが、これは母集団つまり、サンプリングされる大元の全てのデータが存在する集団の平均値という統計学的な意味です。そこからサンプリングされるのが“標本”で、計測される平均値は標本の平均値なのでエックスバー(よく数学で出てくる平均値の記号)がつかわれます。つまり、サンプリングされた標本の平均値から大元の集団(母集団)の平均値を推定するために正規分布が使われるのです。
例えば、サンプリングされたテレビの視聴率から全世帯の視聴率を推定するとか。。。
んで、この式から分かるように、正規分布は平均値とばらつきを表す標準偏差でのみ決まります。決まるというのは、その形が決まります。
ちなみに、平均値が“0”、標準偏差が“1”の正規分布を“標準正規分布(z得点)”といいます。
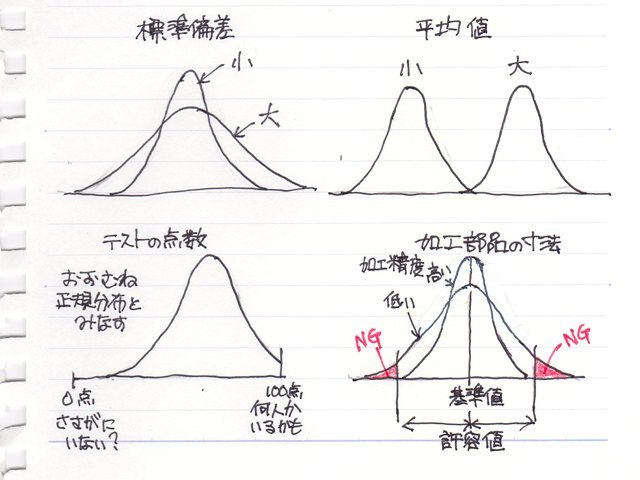
平均値の大小でグラフが左右に移動し、標準偏差の大小で、中心部の高さ、裾の広がり具合が変わります。
もう一つ、xの範囲はマイナスもプラスも無限大(∞)ってことです。
正規分布の例として、テストの成績と書いてあったりしたりします。実際、テストの結果から評価される“偏差値”はテストの結果が正規分布である前提なのですが、この式からみると下は0点、上は満点(100点)で制限されるので、正確には正規分布とは言えないのですが、概ね(おおむね)正規分布とみなされるので問題ありません。
加工部品の寸法のバラつきなんかの場合は、ある許容値の範囲外はNG品としてはじかれてしまっていた場合は次工程に流された部品の寸法のバラつきは正規分布ではなくなるので、注意が必要です。。。
つまり、実際の分布の状況をグラフ等でよく確認する必要があるということですね。
ちなみに、入試の時によく出てくる“偏差値”というのはさっきの平均値“0”、標準偏差“1”の“標準正規分布”を10倍してから50を足して、平均値“50”、標準偏差“10”の正規分布(Z得点)にしたときの全体の中の位置づけのことになります。
んで、実際の計測されたデータがこの式にのっとった正規分布なのかどうかを判断するのは難しいことです。データがたーくさんあるならまだしも、限られたデータではなおさらです。。
そこで、登場するのが“尖度”と“歪度”。これらは、正規分布かどうかを判断する目安に用いられます(あくまで目安です)
また、あらかじめ正規分布になるとわかっている場合、もしそれが正規分布になっていなかったとすると何か異常事態が起こっている可能性があります。
正規分布の範囲と推定
さて、正規分布の場合に何が分かるか、何が推定できるかというと、
平均±標準偏差の範囲(俗に言う±σ)には 全体の約68.26%のデータが含まれる。
平均±2×標準偏差の範囲(±2σ)には、全体の約95.44%のデータが含まれる。
平均±3×標準偏差の範囲(±3σ)には、全体の99.73%のデータが含まれる。
という特徴があります。
ので、平均値と標準偏差が分かっていると、あるデータが全体の中でどのくらいの範囲に入っているのかが分かります。
例えば、テストの平均点が60点で標準偏差が10点だったとすると約68%の学生の点数は50点から70点の間になることがわかります。
この、範囲と推定はExceの“NORMDIST関数”の累積分布で簡単に求めることができます。
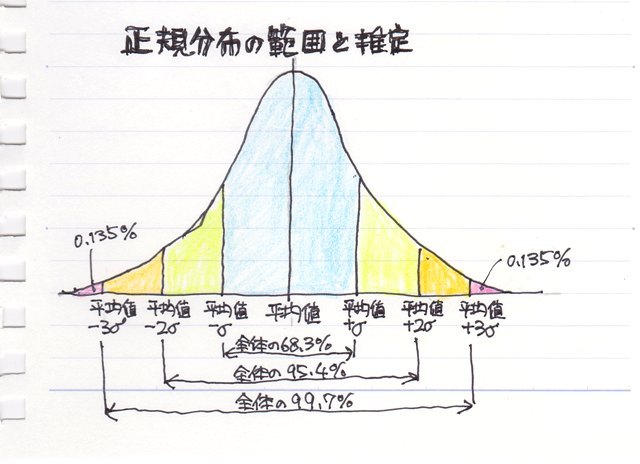
ちなみに、−σ、+σのポイントが確率密度関数の変曲点になります。あっ、変曲点っていうのは読んで字の如く、曲線の曲がる向きが変わるポイントのことです。
では、次回はサイコロ投げをExcelを使ってシミュレーションして正規分布になるかどうか実際にやってみましょう。
![【楽天ブックスならいつでも送料無料】統計学が最強の学問である [ 西内啓 ]](https://hbb.afl.rakuten.co.jp/hgb/?pc=http%3a%2f%2fthumbnail.image.rakuten.co.jp%2f%400_mall%2fbook%2fcabinet%2f2214%2f9784478022214.jpg%3f_ex%3d300x300&m=http%3a%2f%2fthumbnail.image.rakuten.co.jp%2f%400_mall%2fbook%2fcabinet%2f2214%2f9784478022214.jpg%3f_ex%3d80x80) 【楽天ブックスならいつでも送料無料】統計学が最強の学問である [ 西内啓 ] |
関連ページ
尖度と歪度
統計分析の基本中の基本、度数分布表についてまとめてみた
数値データの分布をみるヒストグラムについてまとめてみた
ヒストグラムを層別にしてみると!?
確率の期待値についてまとめてみた
確率についてまとめてみた
データの変動と分散についてまとめてみた
分散と標準偏差について
Excelの統計関数で正規分布の確率密度・累積分布を求める / NORMDIST
Excelの統計関数で尖度を求める / KURT
Excelの統計関数で歪度を求める / SKEW
偏差値について

