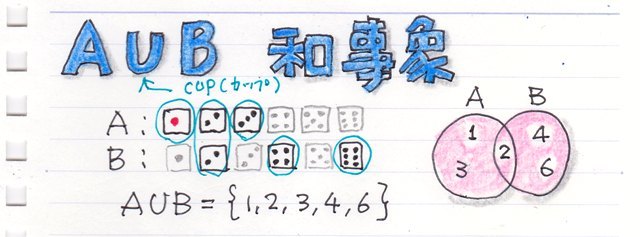
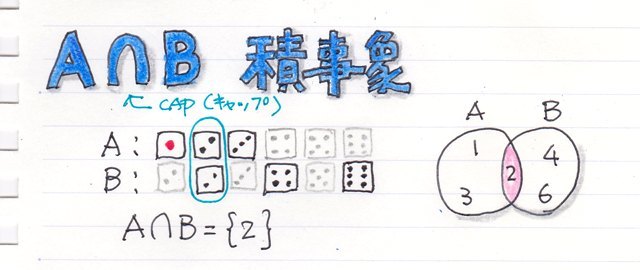
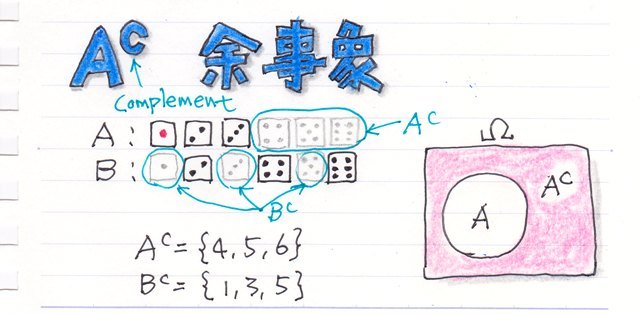
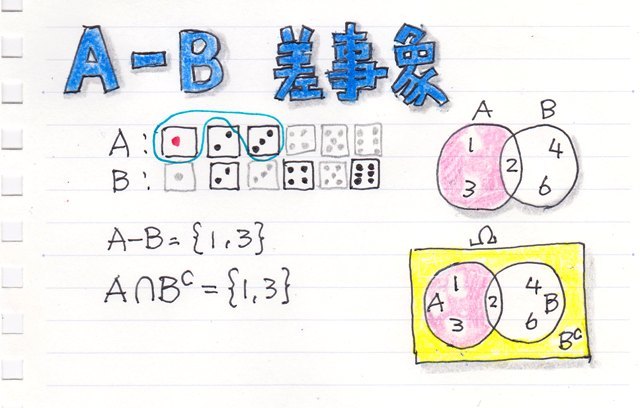
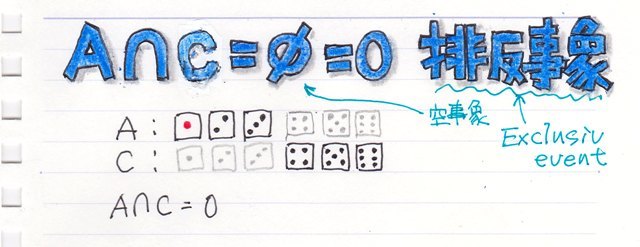
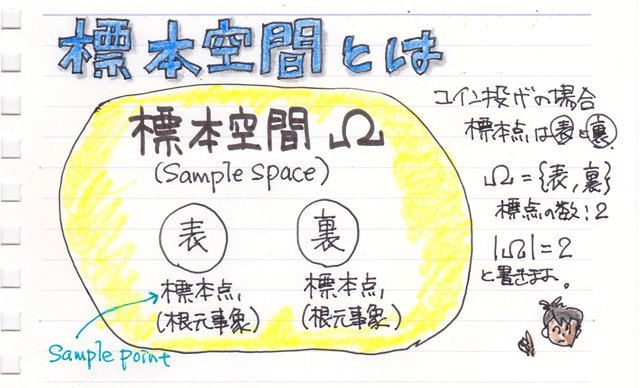
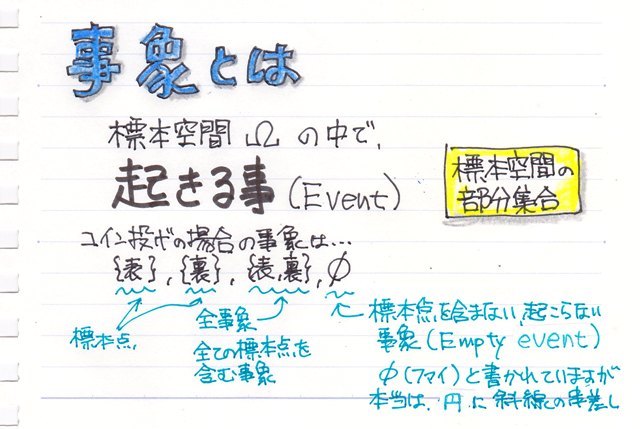
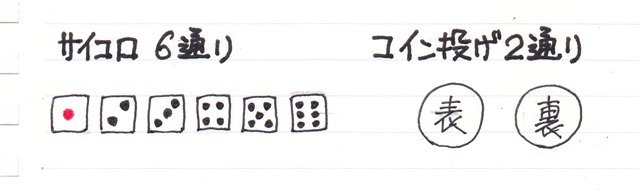
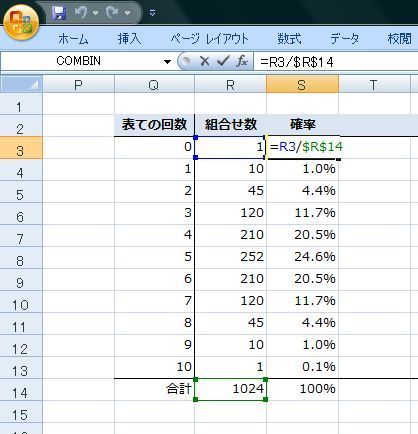
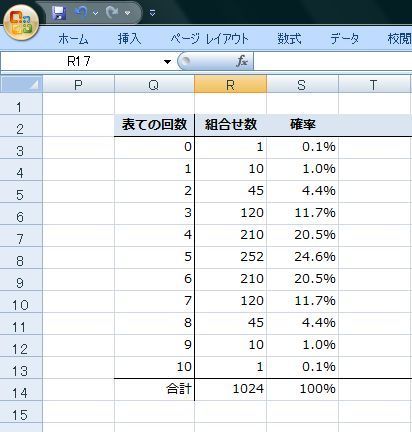
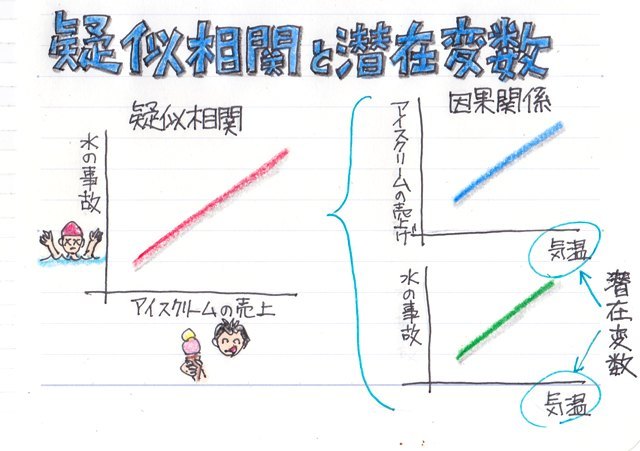
���ڕʂ̓x�����z�ł͂Ȃ����l�f�[�^�̘A�����l�ɑ���x�����z�̃O���t���q�X�g�O�����ƌ����܂��B
�x�����z�\�₻����O���t�������p���[�g�}�͉��������ڂł��̍��ڂł̓x���i�f�[�^�̑傫���j���c���ɕ\���܂��B�܂�A�_�O���t��܂���O���t�ŕ\�킷�悤�ȃf�[�^���ΏۂɂȂ�܂��B
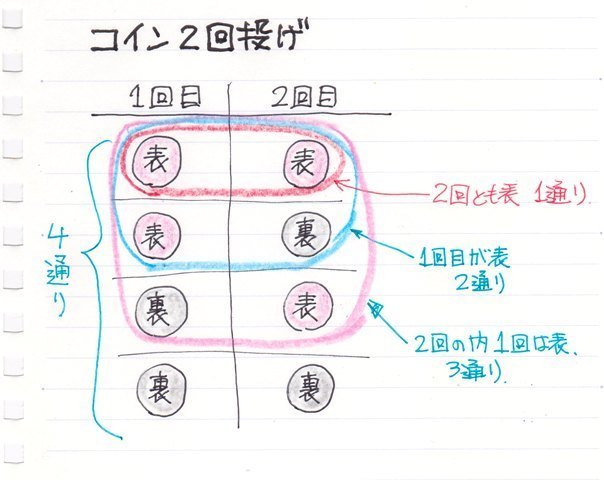
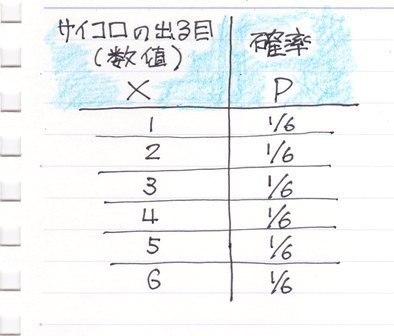
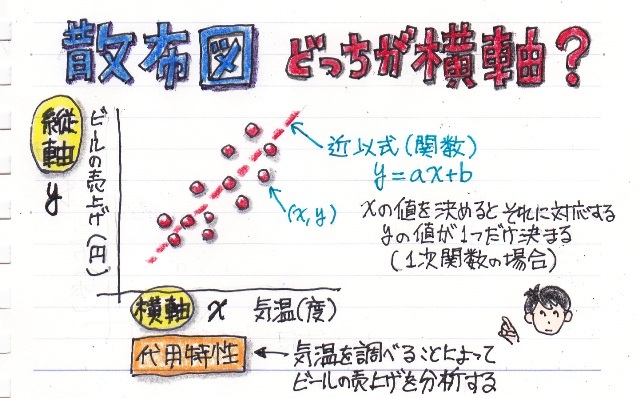
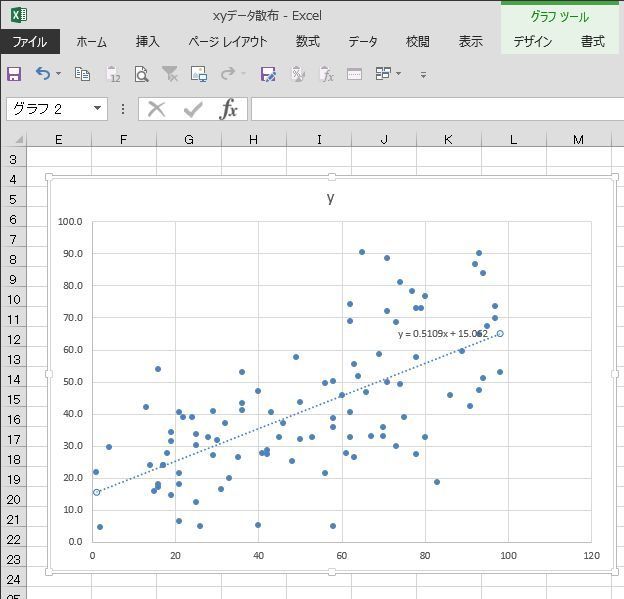
����ɑ��AXY�̎U�z�}�̗l�Ȑ��l�f�[�^�̂���̗l�q��x�����z�Ō���ꍇ�͂ǂ����邩�ƌ����ƁA�����������Ԃŋ�肻�͈̔͂Ɋ܂܂��f�[�^�̌����Ƃ��ēx���Ƃ��ďc���ɕ\���܂��B
��ʓI�Ƀp���[�g�}�̏ꍇ�͗v�����͓��ׂ̈Ɏg�p����邽�߁A�x���̑������ɍ��ڂ����בւ����܂����A�q�X�g�O�����̏ꍇ�͉��������l���̂��߃f�[�^�̕��בւ��͂��ꂸ�A�����ɑ��镪�z�����邱�Ƃɗ��p����܂��B
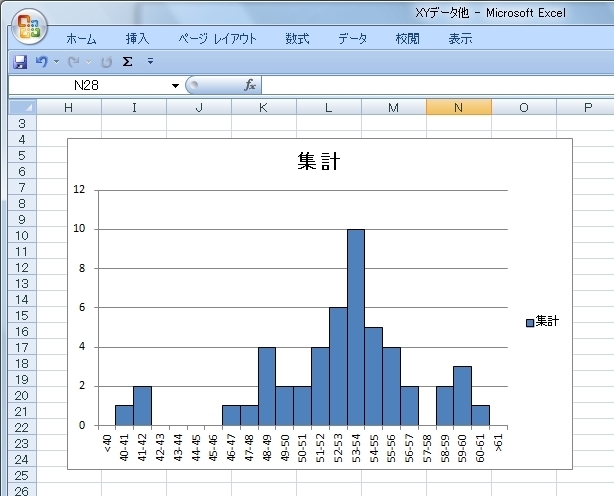
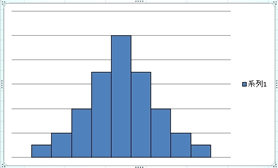
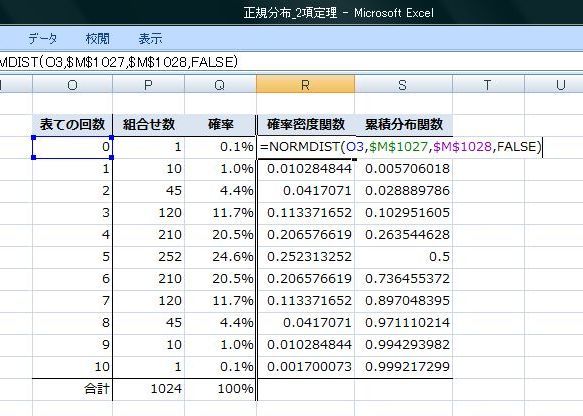
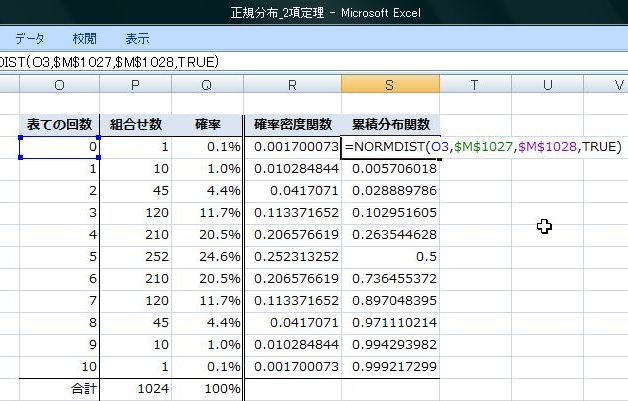
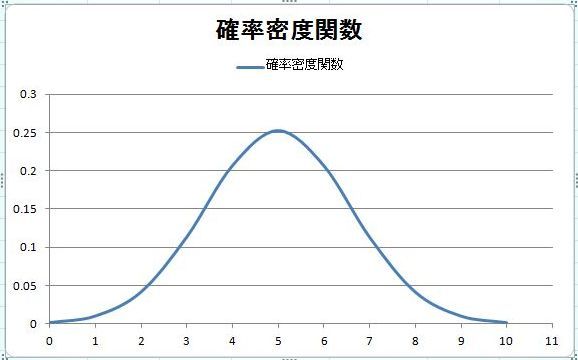
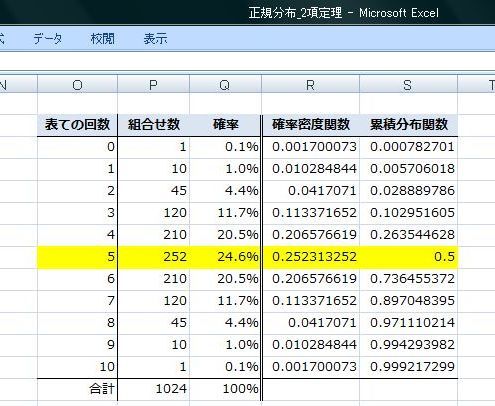
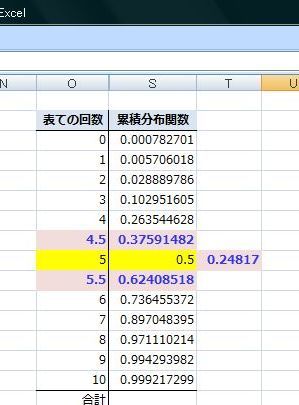
���K���z�f�[�^�����悭�m��ꂽ�q�X�g�O�����ɂȂ�܂��B
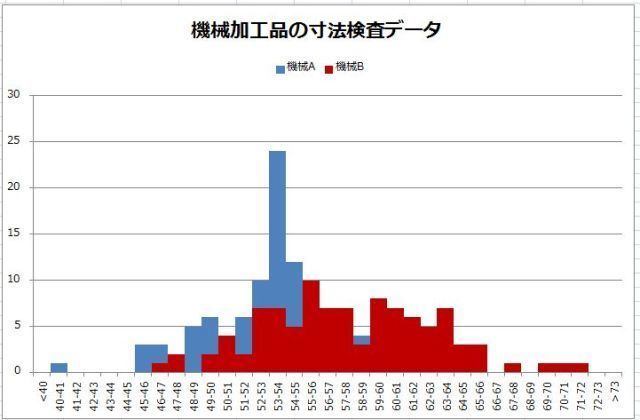
�q�X�g�O�����̌`�i���z�^�j���݂�
�q�X�g�O�����ɂ͕��z�̌`��ŁA�P�����i�R���P�j�Ƒ������i�R���Q�ȏ�j�̑傫���Q�ɕ��ނ���A����ɁA���E�Ώ̂��ǂ����A�O��l�����邩�ǂ����Ȃǂł̕��ނ�����܂��B
1.�P�����ō��E�Ώ�
�f�[�^�̏W�c��������ނ̏ꍇ�́A���z�������͂��̏W�c�̒��̌X�̂���ƌ��Ȃ����Ƃ��o���A��{�I�ɒP�������E�Ώ̂ȕ��z�����܂��܂��B���̕��z�����v�I�ȑ匴���ɂȂ�܂��B
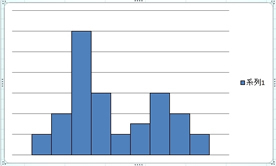
2.������
���̗l�ɎR��2�ȏ゠��̂𑽕����Ƃ����܂��B
���̗l�ȕ��z�̑����͒P�����̕��z���Q�d�Ȃ����ꍇ�Ɍ����܂��B
�܂�A���肵���W�c�ɈقȂ�ʂ̏W�c���܂܂�Ă���悤�ȏꍇ�ɂȂ�܂��B
�R�̍����́A�x���̑傫���ɂł�����A�R�̍����������������肳�ꂽ��ȏW�c�ɂȂ�܂��B
��������A���̗v���ŏW�c��������Ă���̂��������Ă����K�v������܂��B
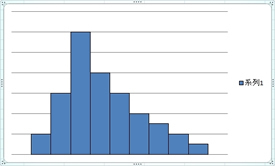
3�D��Ώ́i���E�Ώ̂łȂ��j
�R�𒆐S�ɍ��E�̐��̒������قȂ镪�z���Ώ̂̕��z�ƌ����܂��B�}�̂悤�ɁA�E�ɐ��������ꍇ�ƁA���ɒ����ꍇ������܂��B
���̏ꍇ���������̕ό`�ƌ��邱�Ƃ��ł��܂��B�R�̍������傫���قȂ鑽������2�̎R���߂Â��Ă����Ƃ��̂悤�ȕ��z�ɋ߂Â��܂��B
�]���āA������قȂ�W�c���B��Ă���ƍl���A���̗v���������܂��B
4�D�O��l
�W�c����O�ꂽ�f�[�^��������̂��O��l�Ƃ����܂��B����́A�f�[�^�̓��̓~�X�����đ��̃f�[�^�̍����Ȃǂ̏ꍇ������܂��B
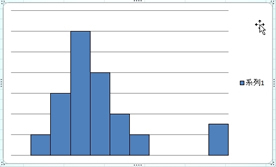
�ƁA���̂悤�Ƀq�X�g�O�������݂Ă��̌`�͂��Ă݂܂��傤�B�������킩�邩���I�H
�ƁA���̂悤�Ƀq�X�g�O�������݂Ă��̌`�͂��Ă݂܂��傤�B�������킩�邩���I�H
���Ȃ݂ɁAExcel�ł̓s�{�b�g�e�[�u�����g���ƊȒP�Ƀq�X�g�O��������鎖���ł��܂��B
����́A�������̗v����������q�X�g�O�����̑w�ʂɂɂ��ĉ�����܂��傤�B
�o�b�N�i���o�[
���v���͂̊�{���̊�{�A�x�����z�\�ɂ��Ă܂Ƃ߂Ă݂�
�֘A�y�[�W
���x���F�x�����z �q�X�g�O����